FUZZY LOGICS IN CONSUMENTEN-ELEKTRONICA + TOEPASSINGEN IN INDUSTRIËLE PROCESBESTURING + OOK IN: VERKEERSMANAGEMENT, BEVEILIGING STROOMNET, (FINANCIËLE) BESLUITVORMING
Nederland dreigt achterop te raken
Vage logica onzichtbaar overal aanwezig
Het deze maand opgerichte DICI (Delft Institute for Computational Intelligence) moet helpen voorkomen dat Nederland achterop raakt in de vage logica, de wiskundige aanpak die tegenwoordig een sterke invloed heeft in de meet- en regeltechniek, maar inmiddels ook zijn invloed doet gelden op veel andere gebieden van wetenschap en technologie, zoals de ontwikkeling van kennissystemen.
– Erwin van den Brink –
De auteur is redacteur van De Ingenieur.
Nederland heeft volgens prof.ir. H.B. Verbruggen van de faculteit Elektrotechniek van de TU Delft ten opzichte van Japan, de VS en Europese landen waaronder vooral Duitsland een achterstand in de toepassing van vage logica of fuzzy logics. In Duitsland zijn grote bedrijven actief op dit gebied zoals Siemens en Klöckner-Müller, maar ook veel kleine bedrijven.
In Nederland valt vooral bij de produktontwikkeling in het midden- en kleinbedrijf nog een hoop zendingswerk te verrichten ondanks inspanningen van instellingen zoals het Centrum voor Micro-Elektronica (CME). DICI beoogt voor bedrijven de weg te effenen naar toepasbare kennis (bij de TU en TNO) over vage logica en meer in het algemeen over computational intelligence.
Wat is vage logica? De wiskundige methode is het eerst toegepast in de regeltechniek. Waarom? Mensen regelen eigenlijk alles vaag, dat wil zeggen niet met exacte waarden. De procesoperator die ’s morgens onder de douche staat regelt volgens de ‘als-dan’-regel die zo kenmerkend is voor vage regeling: ‘Als het water me te heet is, dan meng ik een beetje koud bij’, maar vraag hem niet wat ’te heet’ is en wat ‘een beetje koud’. Als hij om negen uur plaats neemt achter zijn controlepaneel in de zeeppoederfabriek doet hij vaak onbewust iets soortgelijks. Boven in een droogkolom zit een sproeikop die zeepsuspensie in druppels verspreidt die onderin moeten neerdalen als vlokken van ongeveer gelijke grootte; derhalve een proces met vage (namelijk ‘ongeveer’) regelaspecten. Weliswaar is het proces voorzien van een aantal conventionele PID-regelaars (zie Kader), maar een aantal regelkringen wordt door de procesoperator bestuurd.
‘De operators hebben in de loop der jaren zo veel ervaring opgebouwd, dat het proces redelijk in de hand te houden is’, legt Verbruggen uit. ‘Toch gaat het wel eens mis. Er doen zich onvoorziene omstandigheden voor, een operator heeft zijn dag niet, zijn inschatting is onjuist geweest. Als je hem vraagt wat voor regels hij hanteert, dan weet hij dat niet eens precies. Door de operator gade te slaan kunnen we verbanden ontdekken tussen de te regelen grootheden en bepaalde externe omstandigheden zoals temperatuur en vochtigheid. Die verbanden hebben een ‘als-dan’-karakter. Dat is een andere beschrijving dan een fysisch of mathematisch model waaraan technici doorgaans gewend zijn.’
‘Short cut’
De verbanden zijn niet lineair, maar ‘vaag’, rekkelijk, elastisch als het ware, net als in de alledaagse werkelijkheid waar we verbanden aangeven in taal en niet in wiskunde. Verbruggen: ‘Zo’n linguïstisch model kan daarom de werkelijkheid van een proces heel goed beschrijven. Soms is het zelfs de enige mogelijkheid om een systeem te beschrijven. Of het zou volgens de klassieke methode een enorme exercitie zijn. Vertaald in hardware zou dat enorme rekencapaciteit vergen. Vage logica is in die zin een short cut die even goede resultaten oplevert met gebruikmaking van bescheiden modellering en idem dito rekenkracht.’
Voor de moderne industriële procesbesturing is vage logica dan ook bijzonder geschikt. ‘Dank zij toepassing van vage logica kunnen menselijke ervaring en geleidelijkheid van overgangen tussen verschillende regelacties goed in een besturingssysteem worden verwerkt’, aldus Verbruggen.
Elektronische circuits, kleppen, ventielen en motoren kunnen echter niet met deze ‘als-dan’-regels en vage informatie uit de voeten. Zij zijn afhankelijk van harde waarden.
Exacte meetwaarden worden daarom eerst omgezet in vage grootheden zoals ‘heet’, ‘warm’ of ‘koud’. Een besturingssysteem dat werkt met ‘als-dan’-regels gebaseerd op vage logica, neemt dan een ‘vage’ beslissing zoals ‘voeg een beetje koud water toe’. Voor de aansturing van kleppen en ventielen moet die vage beslissing worden vertaald in een hard, crisp, getal: dit heet defuzzificatie, ‘ontvaging’.
Het mooie van vage logica is dat die omzetting van menselijke waarneming en besturing naar kunstmatige besturing veel natuurlijker is, veel meer aansluit bij de wijze waarop wij zelf met kennis omgaan, dan andere vormen van transformatie die voornamelijk zijn gebaseerd op ‘klassieke’ mathematische modellen zoals diffentiaalvergelijkingen .
Soepeler regelgedrag
Fuzzificatie is nodig om de transformatie te verzorgen van het crispe domein (bijvoorbeeld 35 °C) naar het vage domein (warm, heet of aangenaam). Verliezen we dan niet enorm veel informatie? Wel als onze indeling star is, harde grenzen heeft zoals 25…35 °C is aangenaam, 35…50 °C is warm en hoger dan 50 °C is heet. Maar dat is niet zo: vage verzamelingen overlappen elkaar namelijk gedeeltelijk, waardoor een temperatuur zowel aangenaam, warm als heet kan zijn, zij het in verschillende mate. Die mate waarin een temperatuur behoort tot een vage verzameling is een ander kenmerk. In de vage logica heet dat de ‘lidmaatschapsfunctie’ en zij wordt uitgedrukt in een fractioneel getal van 0 tot en met 1. De functie heeft vaak een trapezium- of piramidevorm. Waar de trapezia, dan wel pyramiden, elkaar overlappen, zie je dat oplopende waarden in afnemende mate behoren tot de ene verzameling en in toenemende mate tot de andere: de overgang is geleidelijk, vaag.
Door te rekenen met zulke vage verzamelingen krijg je een over het algemeen soepel regelgedrag. De regeling is rustiger omdat de instelwaarden veel geleidelijker veranderen. Een buschauffeur rijdt ook niet exact midden op de rijbaan, die nooit zuiver kaarsrecht is. Zou hij dat wel doen, dan werden zijn passagiers waarschijnlijk wagenziek van het geslinger. Dergelijk stuurgedrag zien we terug bij handmatige procesbesturing, maar ook in met fuzzy logics geregelde autofocussystemen van (Japanse) video- en fotocamera’s.
Kennissystemen
Japanners waren de eersten die fuzzy logics – ‘foezai’ in Anglojapans – op grote schaal toepasten in (draagbare) consumenten-elektronica. Europeanen pasten eerder al fuzzy logics toe in regelsystemen in de cementindustrie.
Vage logica vergt aanzienlijk minder rekencapaciteit. De benodigde micro-elektronica is daardoor compacter te houden. Verbruggen: ‘Samen met mijnbouwkunde hebben we de slijtage van een trencher, een sleuvengraver, beschreven. Hoe snel de tanden op de graafketting verslijten is afhankelijk van de bodemgesteldheid; die is niet exact te omschrijven, maar duidelijk is wel het causale verband tussen bijvoorbeeld de grootte van de te ontgraven rotsblokken en de slijtagesnelheid: if blocksize is small then bitconsumption is small, waarbij bitconsumption staat voor de slijtage van de graaftanden. Zo hebben we een model gemaakt met zestig regels die heel goed de slijtage beschrijven, zodat je weet hoeveel reserveonderdelen er nodig zijn.’
Ook is vage logica bruikbaar voor expert- en decision support-systemen die redeneren op basis van kennis die gerepresenteerd kan worden in ‘als-dan’-regels. In verzekeringsbedrijven kunnen kennissystemen worden gebruikt voor het berekenen van de risico’s en dus van de premies (zie De Ingenieur, nr. 15 van 27 september 1995, blz. 26-29). Daarnaast is vage logica geschikt voor systemen die vage contouren en patronen moeten herkennen, bijvoorbeeld een systeem dat handgeschreven tekst kan ‘lezen’ of een systeem dat in staat is om op een satellietopname bewolking van een bepaald type te herkennen.
Een dergelijk patroonherkenningssysteem zou weer onderdeel kunnen zijn van een veel groter kennissysteem dat uiteindelijk in staat zal zijn weersverwachtingen te maken, legt dr.ir. J.C.A. van der Lubbe uit. Hij is verbonden aan de vakgroep Informatietheorie van de faculteit Elektrotechniek TU Delft en een van de initiatiefnemers van DICI. Meteorologische kennis, vooral het interpreteren van satellietbeelden, heeft vage aspecten; wanneer is sprake van een wolk, van sluierbewolking en wanneer van heiig weer?
In zo’n kennissysteem wordt, anders dan bij procesbesturing, geen output teruggekoppeld. Het weer valt immers niet te regelen. Er kan wel een terugkoppeling achteraf in worden opgenomen waarbij het systeem kijkt in hoeverre de opgegeven weersverwachting is uitgekomen en waar dat aan ligt. Dit leren kan met bijvoorbeeld neurale netwerken (zie De Ingenieur nr. 20 van 6 december 1994, blz. 6-10), in dit geval fuzzyneurale netwerken (omdat zij niet altijd op vage logica gebaseerd hoeven te zijn).
Achterstand
Van der Lubbe werkt samen met het KNMI (Koninklijk Nederlands Meteorologisch Instituut) en het NLR (Nationaal Lucht- en Ruimtevaartlaboratorium) aan een systeem voor meteorologen dat automatisch weersatellietbeelden interpreteert.
Van der Lubbe: ‘Om te zeggen dat Nederland hopeloos achterloopt is te sterk uitgedrukt, maar in het buitenland is men veel verder. In Duitsland bijvoorbeeld bestaan al veel grote door de overheid gesteunde samenwerkingsverbanden. Daar wordt alles ingezet op vage logica. Het is verbazingwekkend dat wij in Nederland niet voortvarender zijn.’
‘We zijn in Nederland vrij goed in fundamenteel onderzoek, maar vage logica wordt niet als zodanig gezien; als zuiver wiskundige behoor je je er niet mee bezig te houden’, zo verklaart Verbruggen het gebrek aan belangstelling voor vage logica. ‘In Duitsland is men toch pragmatischer. Dat is een land waar spullen gemaakt moeten worden. Vage logica komt daarbij van pas. Wij zijn geen maakland.’ Van der Lubbe denkt dat de Duitse cultuur, waarin men wat filosofischer is ingesteld, een vruchtbaarder bodem is voor vage logica.
Vage logica betekent niet alleen een fundamenteel andere benadering van het oplossen van meet-, regel- en besturingsproblemen, maar is volgens Van der Lubbe ook een breuk in het Westerse Cartesiaanse denken: de tegenstelling tussen enerzijds de werkelijkheid en anderzijds het beeld dat wij hebben van de werkelijkheid; een typische vorm van bipolair denken: iets is waar of niet waar. In het Oosterse denken heeft nooit zoiets bestaan als de klassieke logica. Mogelijk verklaart dat waarom vage logica daar zo’n hoge vlucht heeft genomen.
De fractionele getallen, waarin vage logica uitdrukt in welke mate iets behoort tot een bepaalde verzameling, interpreteren wij westerlingen al gauw als kansgetallen, statistiek: in ons wiskundig denken is gewoon geen plaats voor nuanceringen in termen van ‘een beetje waar’.
Van der Lubbe: ‘Mensen zijn in het dagelijkse leven meesters in het omgaan met vaagheid, maar we leren het af in de wiskunde.’
Toch werd al in de Europese klassieke oudheid behalve aan klassieke logica ook veel gewerkt aan vage logica, door Plato en Aristoteles; Plato onderscheidde gradaties tussen waar en onwaar. Van der Lubbe: ‘Nu langzamerhand het Cartesiaanse denken op de helling wordt gezet, ontstaat ook hier meer ruimte voor vage logica. Alleen binnen de technische universiteiten hebben we daar nog moeite mee. Buiten de TU’s tref je nauwelijks nog Cartesianen aan. Daar is men al lang af van het bipolaire denken in begrippen zoals waar en onwaar.’
(BIJSCHRIFTEN)
(BIJ OPENINGSBEELD DIA HOLLANDSE HOOGTE + OPENGEWERKTE CAMERA)
Op grote schaal werd fuzzy logics voor het eerst toegepast door de Japanners in consumenten-elektronica.
(Foto’s: Roberto Rizzo/HH, Amsterdam; Canon, Hoofddorp)
(QUOTE BIJ PORTRETFOTO)
‘Mensen zijn in het dagelijkse leven meesters in het omgaan met vaagheid, maar we leren het af in de wiskunde’, prof.ir. H.B. Verbruggen (links) en dr.ir. J.C.A. van der Lubbe
(Foto: Michel Wielick, Amsterdam)
(BIJ FOTO 1 EN 2)
Bij TNO en de TU Delft is een robotarm ontwikkeld die wordt bestuurd met vage logica; de arm is een hulpmiddel voor gehandicapten.
(Foto’s: TNO TPD, Delft)
(BIJ FOTO 3)
Met behulp van fuzzy logics is de slijtage van een sleuvengraver beschreven; aan de hand van een model met zestig regels kan worden bekeken hoeveel reserveonderdelen er nodig zijn.
(Foto: Vermeer International, Goes)
(KADER)
Onderzoek
DICI houdt zich bezig met afstemming van onderzoek en onderwijs op het gebied van vage logica, neurale netwerken, neurofuzzy algoritmen, approximate reasoning, fuzzy expertsystemen, genetische en evolutionaire algoritmen en chaotische systemen. DICI richt zich behalve op meet- en regeltechniek en patroonherkenning ook op nieuwe toepassingsgebieden zoals foutdetectie en -diagnose, maatschappelijke problemen, ondersteuning van besluitvorming, financiële beslisproblemen en planning- en schedulingproblemen.
Informatie: prof.ir. H.B. Verbruggen (E-mail: verbruggen@et.tudelft.nl) of dr.ir. J.C.A. van der Lubbe (E-mail: vdlubbe@et.tudelft.nl), TU Delft, faculteit der Elektrotechniek, postbus 5031, 2600 GA Delft, fax (015) 278 66 79.
(KADER)
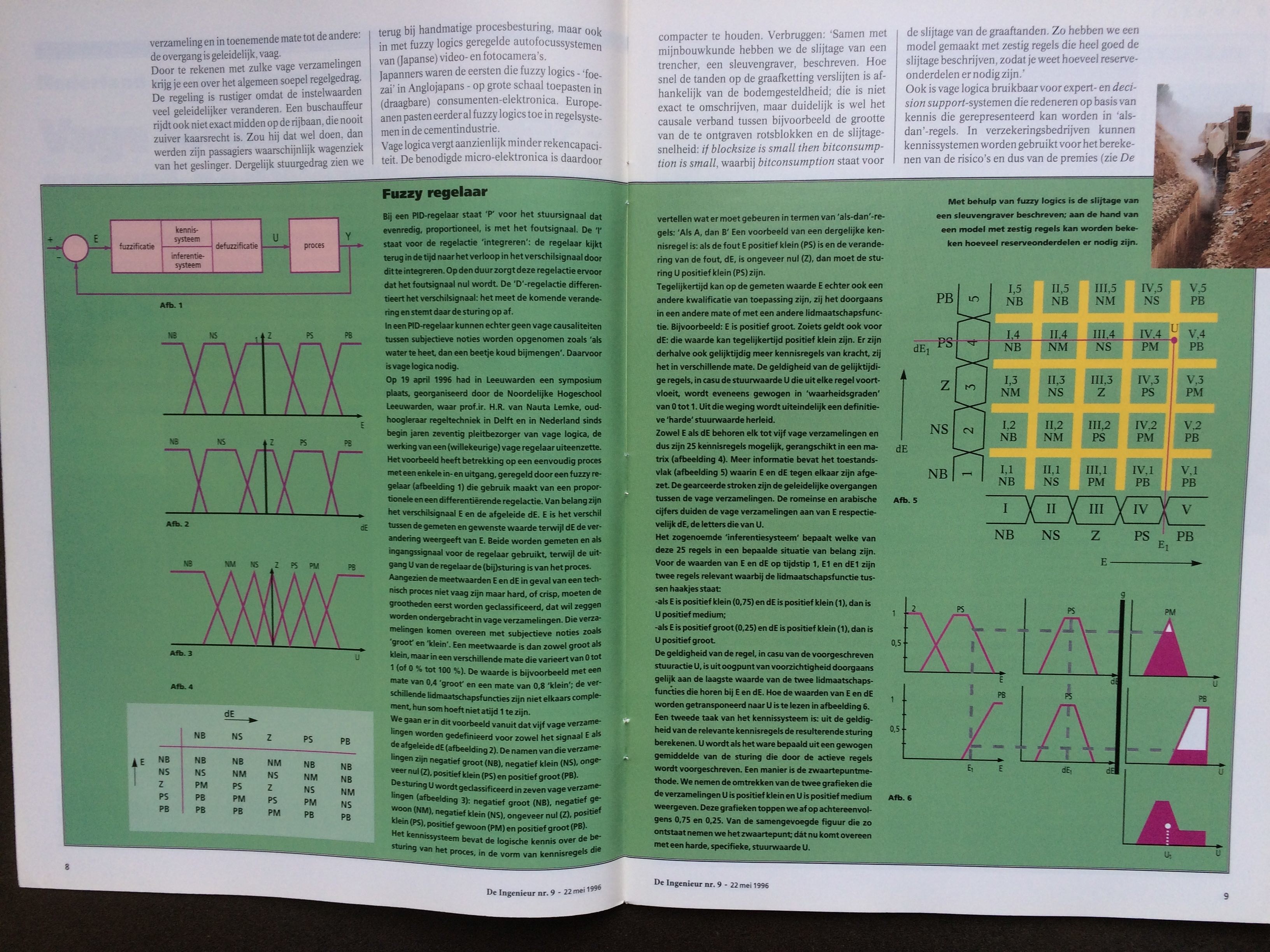
Fuzzy regelaar
Bij een PID-regelaar staat ‘P’ voor het stuursignaal dat evenredig, proportioneel, is met het foutsignaal. De ‘I’ staat voor de regelactie ‘integreren’: de regelaar kijkt terug in de tijd naar het verloop in het verschilsignaal door dit te integreren. Op den duur zorgt deze regelactie ervoor dat het foutsignaal nul wordt. De ‘D’-regelactie differentieert het verschilsignaal: het meet de komende verandering en stemt daar de sturing op af.
In een PID-regelaar kunnen echter geen vage causaliteiten tussen subjectieve noties worden opgenomen zoals ‘als water te heet, dan een beetje koud bijmengen’. Daarvoor is vage logica nodig.
Op 19 april 1996 had in Leeuwarden een symposium plaats, georganiseerd door de Noordelijke Hogeschool Leeuwarden, waar prof.ir. H.R. van Nauta Lemke, oud-hoogleraar regeltechniek in Delft en in Nederland sinds begin jaren zeventig pleitbezorger van vage logica, de werking van een (willekeurige) vage regelaar uiteenzette.
Het voorbeeld heeft betrekking op een eenvoudig proces met een enkele in- en uitgang, geregeld door een fuzzy regelaar (afbeelding 1) die gebruik maakt van een proportionele en een differentiërende regelactie. Van belang zijn het verschilsignaal E en de afgeleide dE. E is het verschil tussen de gemeten en gewenste waarde terwijl dE de verandering weergeeft van E. Beide worden gemeten en als ingangssignaal voor de regelaar gebruikt, terwijl de uitgang U van de regelaar de (bij)sturing is van het proces.
Aangezien de meetwaarden E en dE in geval van een technisch proces niet vaag zijn maar hard, of crisp, moeten de grootheden eerst worden geclassificeerd, dat wil zeggen worden ondergebracht in vage verzamelingen. Die verzamelingen komen overeen met subjectieve noties zoals ‘groot’ en ‘klein’. Een meetwaarde is dan zowel groot als klein, maar in een verschillende mate die varieert van 0 tot 1 (of 0 % tot 100 %). De waarde is bijvoorbeeld met een mate van 0,4 ‘groot’ en een mate van 0,8 ‘klein’; de verschillende lidmaatschapsfuncties zijn niet elkaars complement, hun som hoeft niet atijd 1 te zijn.
We gaan er in dit voorbeeld vanuit dat vijf vage verzamelingen worden gedefinieerd voor zowel het signaal E als de afgeleide dE (afbeelding 2). De namen van die verzamelingen zijn negatief groot (NB), negatief klein (NS), ongeveer nul (Z), positief klein (PS) en positief groot (PB).
De sturing U wordt geclassificeerd in zeven vage verzamelingen (afbeelding 3): negatief groot (NB), negatief gewoon (NM), negatief klein (NS), ongeveer nul (Z), positief klein (PS), positief gewoon (PM) en positief groot (PB).
Het kennissysteem bevat de logische kennis over de besturing van het proces, in de vorm van kennisregels die vertellen wat er moet gebeuren in termen van ‘als-dan’-regels: ‘Als A, dan B’ Een voorbeeld van een dergelijke kennisregel is: als de fout E positief klein (PS) is en de verandering van de fout, dE, is ongeveer nul (Z), dan moet de sturing U positief klein (PS) zijn.
Tegelijkertijd kan op de gemeten waarde E echter ook een andere kwalificatie van toepassing zijn, zij het doorgaans in een andere mate of met een andere lidmaatschapsfunctie. Bijvoorbeeld: E is positief groot. Zoiets geldt ook voor dE: die waarde kan tegelijkertijd positief klein zijn. Er zijn derhalve ook gelijktijdig meer kennisregels van kracht, zij het in verschillende mate. De geldigheid van de gelijktijdige regels, in casu de stuurwaarde U die uit elke regel voortvloeit, wordt eveneens gewogen in ‘waarheidsgraden’ van 0 tot 1. Uit die weging wordt uiteindelijk een definitieve ‘harde’ stuurwaarde herleid.
Zowel E als dE behoren elk tot vijf vage verzamelingen en dus zijn 25 kennisregels mogelijk, gerangschikt in een matrix (afbeelding 4). Meer informatie bevat het toestandsvlak (afbeelding 5) waarin E en dE tegen elkaar zijn afgezet. De gearceerde stroken zijn de geleidelijke overgangen tussen de vage verzamelingen. De romeinse en arabische cijfers duiden de vage verzamelingen aan van E respectievelijk dE, de letters die van U.
Het zogenoemde ‘inferentiesysteem’ bepaalt welke van deze 25 regels in een bepaalde situatie van belang zijn. Voor de waarden van E en dE op tijdstip 1, E1 en dE1 zijn twee regels relevant waarbij de lidmaatschapsfunctie tussen haakjes staat:
-als E is positief klein (0,75) en dE is positief klein (1), dan is U positief medium;
-als E is positief groot (0,25) en dE is positief klein (1), dan is U positief groot.
De geldigheid van de regel, in casu van de voorgeschreven stuuractie U, is uit oogpunt van voorzichtigheid doorgaans gelijk aan de laagste waarde van de twee lidmaatschapsfuncties die horen bij E en dE. Hoe de waarden van E en dE worden getransponeerd naar U is te lezen in afbeelding 6.
Een tweede taak van het kennissysteem is: uit de geldigheid van de relevante kennisregels de resulterende sturing berekenen. U wordt als het ware bepaald uit een gewogen gemiddelde van de sturing die door de actieve regels wordt voorgeschreven. Een manier is de zwaartepuntmethode. We nemen de omtrekken van de twee grafieken die de verzamelingen U is positief klein en U is positief medium weergeven. Deze grafieken toppen we af op achtereenvolgens 0,75 en 0,25. Van de samengevoegde figuur die zo ontstaat nemen we het zwaartepunt; dát nu komt overeen met een harde, specifieke, stuurwaarde U.
(BIJSCHRIFTEN TEKENINGEN KADER)
Afb. 1
Afb. 2
Afb. 3
Afb. 4
Afb. 5
Afb. 6